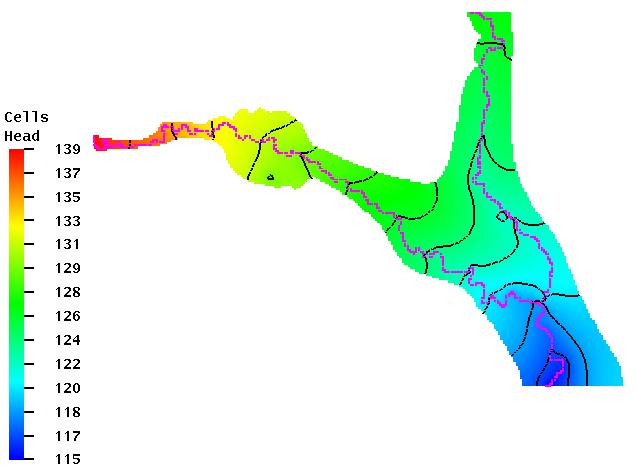
A fentiek tükrében és a szemléletnek megfelelôen a folyóvölgyekben uralkodó felszín alatti vízmozgás a felszíni lefolyás, illetve a vízkivételek körüli depresszió irányába történik (4. ábra).
Az elôzetes modell által a figyelôkutak helyén számított eredmények átlagosan kevesebb, mint 1 m-rel térnek el a mért értékektôl (5. ábra, 1. táblázat). Az ábrán piros kör jelöli a számítottnál magasabb, kék négyzet az alacsonyabb értékeket. A jelek mérete arányos a hozzájuk tartozó különbségekkel. A néhány, ennél nagyobb eltérés okára (pl. a TM-20 és TM-28 jelû kutak helyén) visszatérünk. A vízbázisok körüli 50 éves hozzáfolyási terület az áramvonalak burkológörbéjeként értelmezhetô.
kút különbség [m] kút különbség [m] kút különbség [m] 17/1 -0.1 40 2.4 42 0.1 44 -1.1 45 -2.0 46 -2.3 47 -1.7 48 -1.3 49 -1.5 51 -2.3 E1 0.3 E2 0.3 E4 -0.9 E5 0.0 H2 -0.6 H3 1.0 M2 2.7 TM-2 -0.7 TM-4 -0.2 TM-6 0.6 TM-7 0.2 TM-8 0.6 TM-9 0.6 TM-11 0.2 TM-12 -0.4 TM-14 0.2 TM-15 0.5 TM-16 1.1 TM-17 0.2 TM-20 3.6 TM-21 3.4 TM-22 1.4 TM-28 -2.4 TM-32 -0.7 TM-33 0.8 TM-34 0.4 TM-35 -0.3 TM-36 0.0 TM-41 0.4 TM-42 -0.5 TM-43 -0.1 TM-44 0.1 TT-1 0.1 TT-4 -1.2 TT-9 0.4 TT-10 0.2 TT-11 -0.8 TT-12 3.5 TT-13 3.3 V1 0.0 V2 -2.6 V3 0.1 K5 0.6 K2 1.1 K7 0.6 M8 1.2 M5 0.4 M1 0.5 K4 0.7 K8 0.8 K15 1.4
Megjegyezzük, hogy annak a feltételezésnek, amely szerint a csapadékból származó beszivárgás az egész területen egységesen felülmúlja az evapotranspirációt, az adott idejû hozzáfolyási terület alakjára nézve fontos következményei vannak. Tekintsük ugyanis a kétdimenziós modell egy vonalmenti metszetét, a fenti numerikus modellnek megfelelô peremfeltételekkel (6. ábra). Az x1 < x < x4 tartományban elterülô kavicsteraszt valamely K1 szivárgási tényezô jellemzi, a tartományon kívül esô közeg az egyszerûség kedvéért tökéletesen vízzáró ( K(x<x1) = 0.0 és K(x>x4) = 0.0). Ez utóbbi feltétel azt jelenti, hogy a kavicsterasz szélén a hozzáfolyás nulla (Q(x=x1) = Q(x=x4) = 0.0). A kavicsteraszon belül két ponton - a folyók helyén - rögzítjük a vízszintet (h(x=x2) = h2 és h(x=x3) = h3). A talajvíztükör alakját mármost csak a B beszivárgás és az E evapotranspiráció befolyásolják: ha a beszivárgás nagyobb, a talajvíztükör felülrôl domború (t1), ha az evapotranspiráció a nagyobb, a talajvíztükör felülrôl homorú a peremfeltételek közötti szakaszokon. A talajvíztükör mindkét esetben vízszintes érintôvel csatlakozik a kavicsterasz vízzáró széleihez.
Ha egy áramvonalat a közölt algoritmus (Függelék A) szerint, a nyelôtôl visszafelé próbálunk megrajzolni, akkor - a nyomás gradiensének irányába mozogva - domború talajvíztükör esetében elôbb-utóbb az áramvonal fel fog kapaszkodni vagy a két folyó közti talajvízdombra (mint a Borsodszirák I vízmûtôl indított áramvonalak nyugati nyalábja), vagy a kavicsterasz szélére. A talajvízdombon vagy -háton az áramvonal a legmagasabb pontok mentén nyilván a kavics széléig fog haladni.
Mivel az áramlás egy vízzáró fal mentén a fallal párhuzamos, azt várhatnánk, hogy a továbbiakban az áramvonal a kavics széle mentén kúszik egyre magasabbra, egészen a modell széléig, vagy addig, amíg a rendelkezésére álló idô el nem fogy (Függelék A). A fenti numerikus modell azonban numerikus hibákkal terhelt, amelyek egyik megnyilvánulása, hogy a kavicsterasz legszélsô elemeiben a gradiens nem párhuzamos a kavics szélével, hanem abból kifelé mutatva az áramvonalat a vízzáró zónába hajtja (7. ábra). A vízzáró zónában az algoritmus megállítja az áramvonalat (Függelék A).
(Megjegyezzük, hogy a kavics szélének, mint peremnek a pontosabb követésével és a szivárgási sebességmezô folytonossá tételével [2] ez a probléma teljesen kiküszöbölhetô: ekkor az áramvonal nem lép ki a vízvezetô közegbôl, hanem annak legszélsô elemeiben folytatja az útját.)
Mindebbôl az következik, hogy ha a fenti numerikus modellben egy áramvonal T1 idô alatt eléri a kavicsterasz szélét, és ott megáll, akkor hiába bocsájtunk T > T1 több idôt a rendelkezésére, az alakja változatlanul a T1 idô alatt megtett utat fogja megjeleníteni.
Az fent bemutatott 50 éves hozzáfolyási területet az áramvonalnyaláb valójában már 10-30 év alatt bejárja. A 100 éves hozzáfolyási terület alakja így nem különbözik az 50 éves hozzáfolyási terület alakjától.
Amennyiben az evapotranspiráció mértéke felülmúlja a beszivárgásét, azaz a telített zóna a térszínen kereszül vizet veszít, úgy a nyelôkbôl indított áramvonalak elôbb-utóbb eljutnak a függômederben folyó felszíni vizekig (6. ábra, t2 talajvíztükör), mint forrásokig. Az áramvonal ezután a meder vonalát követve halad a vízfolyás forrásáig vagy a modell széléig.
A legalább egy, illetve öt éves hozzáfolyási területeket a modell néhány száz hektárnyinak mutatja (8-9. ábrák).